A fabricação aditiva permite a produção de componentes funcionalmente otimizados com alta complexidade geométrica, a oportunidade de utilizar geometrias irregulares para o enchimento como seja duma geometria porosa como parte integrante do processo de produção é um exemplo dum recurso de fabricação aditiva exclusiva. Métodos do desenho técnico automatizados são ainda incapazes de explorar plenamente essa liberdade do desenho de produto. Neste post tentarei mostrar como abordar a otimização de topologia fornecendo um meio de desenhar e projetar componentes baseados num preenchimento que possuam ter uma carga de resistência mecânica fortemente melhorada e como resultado uma estabilidade estrutural melhorada.
Trabalhos recentes demonstraram que o material no interior do produto dum modelo 3D pode ser desenhado para fazer com que a produção duma reprodução fabricada satisfaça demandas específicas da aplicação nas suas propriedades físicas assim como a resistência a cargas externas. Uma prática amplamente utilizada para fabricar tais modelos é a fabricação de aditivos à base de camadas da fabricação aditiva que, no entanto, sofre dum problema de adição e remoção das estruturas de suporte interiores.
Trabalhos recentes demonstraram que o material no interior do produto dum modelo 3D pode ser desenhado para fazer com que a produção duma reprodução fabricada satisfaça demandas específicas da aplicação nas suas propriedades físicas assim como a resistência a cargas externas. Uma prática amplamente utilizada para fabricar tais modelos é a fabricação de aditivos à base de camadas da fabricação aditiva que, no entanto, sofre dum problema de adição e remoção das estruturas de suporte interiores.
A apresentação dum novo método para gerar estruturas de enchimento específicas de aplicação em células especificas de modo que as estruturas resultantes podem satisfazer automaticamente as exigências de fabrico sobre o ângulo de saliência e a espessura da parede. Estruturas de suporte adicionais podem ser evitadas inteiramente nalgumas estruturas, para conseguir isso pode-se introduzir a utilização de uma célula elástica e adaptativa, que é construída a partir de um modelo de superfície de entrada. Partindo do conjunto escasso inicial de células especiais por meio de técnicas de otimização numéricas, uma função objetiva pode ser melhorada subdividindo adaptativamente essa célula especial e assim adicionando mais paredes em células. A demonstração da eficácia deste nosso método para gerar desenhos do interior de um produto para melhorar as aplicações de rigidez mecânica e a sua estabilidade estática.
1-Introdução
A fabricação de aditiva permite a fabricação de componentes com complexidade geométrica, muito além do que pode ser alcançado com as tecnologias de fabricação convencionais. A otimização da topologia que é particularmente conhecida por criar componentes mecânicos leves nas indústrias aeroespacial e automóvel, fornecendo um meio para inteligentemente explorar essa liberdade do desenho técnico mecânico, tornando estas duas tecnologias um ajuste ideal, mas até agora as abordagens de optimização de topologia só foram adaptadas em menor grau às novas oportunidades e às restrições de fabrico relevantes para a fabricação aditiva.
1-Introdução
A fabricação de aditiva permite a fabricação de componentes com complexidade geométrica, muito além do que pode ser alcançado com as tecnologias de fabricação convencionais. A otimização da topologia que é particularmente conhecida por criar componentes mecânicos leves nas indústrias aeroespacial e automóvel, fornecendo um meio para inteligentemente explorar essa liberdade do desenho técnico mecânico, tornando estas duas tecnologias um ajuste ideal, mas até agora as abordagens de optimização de topologia só foram adaptadas em menor grau às novas oportunidades e às restrições de fabrico relevantes para a fabricação aditiva.
IMAGEM01b
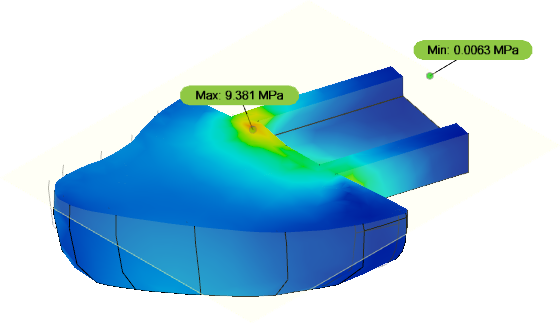
O preenchimento é um exemplo de uma característica única dos métodos de fabricação aditiva por extrusão, que permite a criação de estruturas que são compostas por uma casca exterior sólida e um interior intersticial como se observa na IMAGEM01, também pode ser chamada duma abordagem de revestimento para otimização de topologia.
Enquanto a otimização da topologia padrão se aproxima para a produção de estruturas sólidas como se observa na IMAGEM01a, a abordagem de revestimento resulta em estruturas com uma casca sólida e um interior poroso, exatamente como se utilizaria no enchimento como se observa na IMAGEM1b. A abordagem do revestimento não oferece uma melhoria da rigidez, mas, no entanto, como mostrado neste estudo resulta numa peça fortemente melhorada o que é um elemento importante de estabilidade estrutural. Assim se tentará demonstrar o grande potencial duma adaptação da otimização da topologia para fabricação aditiva.
Os componentes optimizados por topologia obtidos através duma abordagem de conformidade mínima padrão não deve de ter importância, pelo contrário a abordagem resulta em configurações denominadas de tensão e ou compressão e evita membros de flexão.
Como a carga de encurvadura está estreitamente relacionada com a rigidez à flexão sendo proporcional para o caso simples da encurvadura de Euler estas estruturas podem muito bem acabar por ser falha limitada pela carga de encurvadura em vez da resistência à fratura do material, e o problema torna-se cada vez mais pronunciada para frações de menor volume.
Diferentes trabalhos têm tratado a possibilidade de incluir uma restrição na encurvadura para resolver os problemas em conformidade na otimização da topologia. As abordagens sugeridas até agora, no entanto não produziram resultados convincentes ou são desafiadas pelo agrupamento dum elevado número de modos próprios no auto valor mais baixo da carga de encurvamento. Esse agrupamento implica a necessidade de computar um grande número de auto valores, levando a uma carga computacional perigosamente pesada. Em vez disso a análise de encurvamento obrigatório é normalmente realizada como uma etapa pós-otimização ao invés de como uma restrição de otimização integrada. Se se verificar que a estabilidade elástica do componente é insuficiente pode ser aplicado um pós-processamento para melhorar a carga mínima de encurvadura; contudo este processo pode conduzir a componentes sub óptimos.
A natureza proporciona uma série de exemplos de estruturas que têm uma carga de curvatura intrinsecamente elevada em comparação com o peso e a maioria dos exemplos óbvios são os ossos e as esturras das plantas que são compostas por uma casca externa rígida e sólida com um interior mais macio e poroso, o mesmo conceito é explorado em estruturas em sanduíche que são caracterizadas de forma semelhante por uma elevada rigidez à flexão em peso e assim, uma elevada carga de encurvadura. A elevada carga de encurvadura das estruturas obtidas com a técnica de revestimento com os mesmos princípios, conforme demonstrado neste trabalho a abordagem de revestimento oferece uma forma eficaz e computacionalmente barata de tornar a vantagem do enchimento da fabricação aditiva e assim assegurar uma carga de encurvadura elevada.
2 – Processos
Continuação – https://rishivadher.blogspot.pt/2017/04/otimizacao-da-topologia-para-impressao_30.html
Enquanto a otimização da topologia padrão se aproxima para a produção de estruturas sólidas como se observa na IMAGEM01a, a abordagem de revestimento resulta em estruturas com uma casca sólida e um interior poroso, exatamente como se utilizaria no enchimento como se observa na IMAGEM1b. A abordagem do revestimento não oferece uma melhoria da rigidez, mas, no entanto, como mostrado neste estudo resulta numa peça fortemente melhorada o que é um elemento importante de estabilidade estrutural. Assim se tentará demonstrar o grande potencial duma adaptação da otimização da topologia para fabricação aditiva.
Os componentes optimizados por topologia obtidos através duma abordagem de conformidade mínima padrão não deve de ter importância, pelo contrário a abordagem resulta em configurações denominadas de tensão e ou compressão e evita membros de flexão.
Como a carga de encurvadura está estreitamente relacionada com a rigidez à flexão sendo proporcional para o caso simples da encurvadura de Euler estas estruturas podem muito bem acabar por ser falha limitada pela carga de encurvadura em vez da resistência à fratura do material, e o problema torna-se cada vez mais pronunciada para frações de menor volume.
Diferentes trabalhos têm tratado a possibilidade de incluir uma restrição na encurvadura para resolver os problemas em conformidade na otimização da topologia. As abordagens sugeridas até agora, no entanto não produziram resultados convincentes ou são desafiadas pelo agrupamento dum elevado número de modos próprios no auto valor mais baixo da carga de encurvamento. Esse agrupamento implica a necessidade de computar um grande número de auto valores, levando a uma carga computacional perigosamente pesada. Em vez disso a análise de encurvamento obrigatório é normalmente realizada como uma etapa pós-otimização ao invés de como uma restrição de otimização integrada. Se se verificar que a estabilidade elástica do componente é insuficiente pode ser aplicado um pós-processamento para melhorar a carga mínima de encurvadura; contudo este processo pode conduzir a componentes sub óptimos.
A natureza proporciona uma série de exemplos de estruturas que têm uma carga de curvatura intrinsecamente elevada em comparação com o peso e a maioria dos exemplos óbvios são os ossos e as esturras das plantas que são compostas por uma casca externa rígida e sólida com um interior mais macio e poroso, o mesmo conceito é explorado em estruturas em sanduíche que são caracterizadas de forma semelhante por uma elevada rigidez à flexão em peso e assim, uma elevada carga de encurvadura. A elevada carga de encurvadura das estruturas obtidas com a técnica de revestimento com os mesmos princípios, conforme demonstrado neste trabalho a abordagem de revestimento oferece uma forma eficaz e computacionalmente barata de tornar a vantagem do enchimento da fabricação aditiva e assim assegurar uma carga de encurvadura elevada.
2 – Processos
Continuação – https://rishivadher.blogspot.pt/2017/04/otimizacao-da-topologia-para-impressao_30.html

Sem comentários:
Enviar um comentário